Quick Specs
The database and tools are divided into three levels so that students can access a suitable level of information as they progress through their studies, from pre-university up to postgraduate courses.
Ansys Granta EduPack—formerly CES EduPack—is a unique set of teaching resources that help academics enhance courses related to materials across engineering, design, science and sustainable development.
Granta EduPack, formerly CES EduPack, is a unique set of teaching resources to support materials education.
Granta EduPack provides support to enhance undergraduate materials education. EduPack includes a database of materials and process information, materials selection tools and a range of supporting resources. EduPack is divided into three levels so that students can access a suitable level of information as they progress through their studies.
Granta EduPack has also been designed to support a wide variety of teaching styles, from the design- and science-led approaches to problem-based teaching.
The database and tools are divided into three levels so that students can access a suitable level of information as they progress through their studies, from pre-university up to postgraduate courses.
July 2023
We’re supporting students to learn to make the best decisions around materials and sustainability.

Improved material selection for environmental performance with updates to CO2 footprint and embodied energy in MaterialUniverse™. Updated data on Nations in Conflict within the Sustainability databases to enhance social sustainability analyses.
Use our new help site to get the most out of Granta EduPack - directly linked to the software. Our improved search function makes finding key topics easy. Find out how to use key features and the enhanced material selection or just how to use Granta EduPack best.

We've updated the Global Polymers Plastics table, including new test data, manufacturer data (SABIC, Kuraray, MOCOM), environmental end-of-life attributes, and non-linear data for simulation.
CAPABILITIES
Granta EduPack provides the tools to help engage your students by using interactive, visual software. It is available in two versions: Granta EduPack, which contains all data and tools; and Granta EduPack Introductory, which contains a subset of data and tools intended for teaching introductory courses.
Both versions are divided into three levels so that students have access to appropriate materials information as their studies progress. At all levels, Granta EduPack provides students with a comprehensive database of materials and process information that is always kept up to date. In addition, self-study resources are available to stretch stronger students and to help others catch up, providing a flexible tool for every educator to utilize.
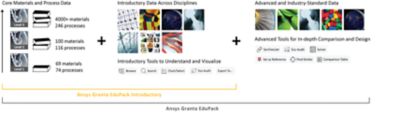
Essential features to support materials education, included in both Granta EduPack and Granta EduPack Introductory.
Enhanced features to support advanced learning and capstone design projects, only available in the full version of Granta EduPack
The Granta EduPack databases contain an unrivalled library of materials information. Draw on materials data at a level suitable for your students and courses.
Granta EduPack contains powerful materials selection and charting tools. These are designed to make it easy to learn and apply the rational selection methodology pioneered by Prof. Mike Ashby at the University of Cambridge.
Help students think critically and evaluate the environmental impact of a product. With the Eco Audit Tool, students can test design scenarios and understand the importance behind materials and process choices.
Find inspiration for your teaching and access case studies, exercises, active teaching packages and more.
Granta EduPack includes models for predicting the properties of hybrid materials, enabling comparison with conventional materials and for predicting part costs. You can add your own models and apply the results to property charts.
Additional databases featuring industry standard data for advanced study and capstone projects.
Granta EduPack includes models for predicting the properties of hybrid materials, enabling comparison with conventional materials and for predicting part costs. You can add your own models and apply the results to property charts.
Set reference materials, adjust nearness settings to find similar materials, and view material options in a comparison table
Consider cost modelling within life cycle comparisons, allowing trade-offs between economic and environmental considerations.
It's vital to Ansys that all users, including those with disabilities, can access our products. As such, we endeavor to follow accessibility requirements based on the US Access Board (Section 508), Web Content Accessibility Guidelines (WCAG), and the current format of the Voluntary Product Accessibility Template (VPAT).